Calculus

Calculus is the study of how things change. It provides an overall framework for the analysis of change. As we will see, the ability to probe how things change is essential in the optimisation of machine learning algorithms. Furthermore, a conceptual understanding of all areas of calculus will help our appreciation of data science methods.

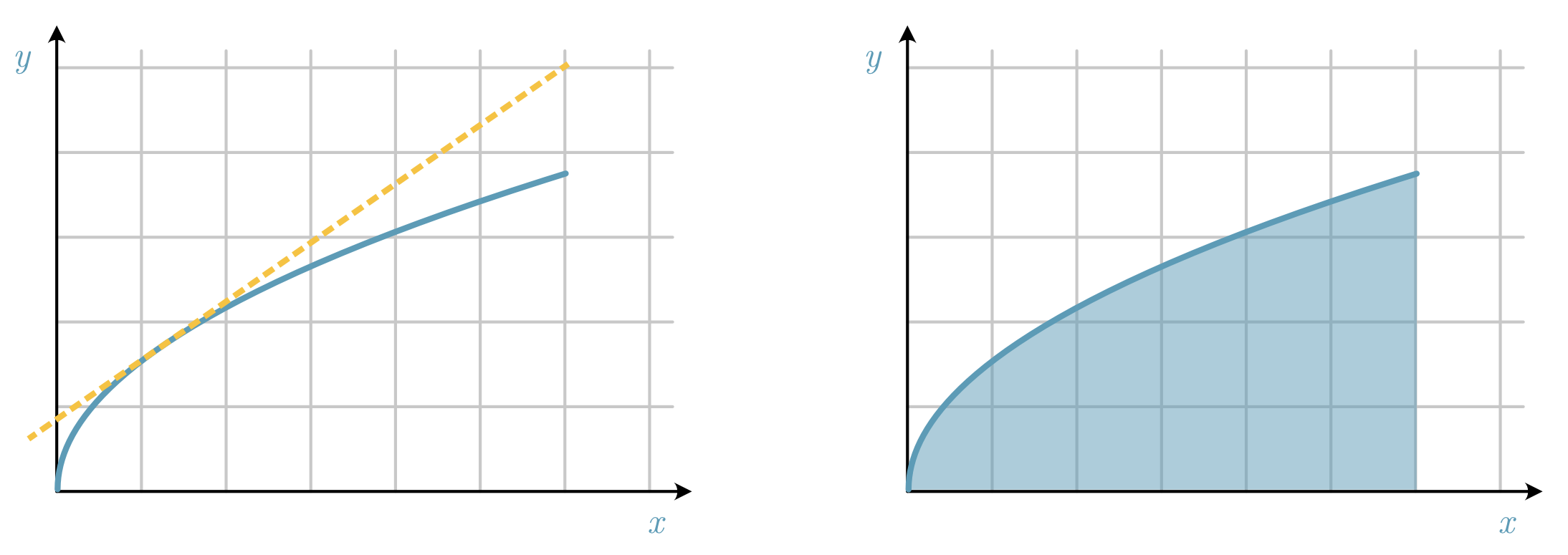
Fig. 18 The core components of calculus for the function \(y\) (solid blue line); (left) the derivative of \(y\) with respect to \(x\) gives the gradient of the dashed yellow line, which is a tangent of \(y\) and (right) the integral of \(y\) can be used to calculate the area under \(y\) (shaded in blue).

The core components of calculus are differentiation, which describes the rate of change of some function, and integration, which handles accumulation when some variable changes. These two concepts are often taught as opposites; this section will examine why this is.

A popular example that is used to talk about calculus is where you know the position of a car as a function of time. The derivative of position with respect to time will give the velocity (speed) of the car. However, if we know the velocity as a function of time, we can find the position by integration.

Further Reading

To get a more fundamental understanding of calculus, I highly recommend the 3Blue1Brown video series on the subject. You can find the series playlist on YouTube.