SciPy Statistical Objects

SciPy Statistical Objects#

The SciPy library has some fantastic functionality for working with statistical objects. Specifically, here we will look at the scipy.stats.rv_continuous base class (and the discrete sibling, scipy.stats.rv_discrete). This base class is used to gain access to a range of functionality for different statistical distributions. We can find a full list of the distributions that can be modelled in the SciPy documentation.

Discrete Distributions#

We will start by looking at the bernoulli distribution. This can be imported as follows.

from scipy.stats import bernoulli

The Bernoulli distribution has a single parameter, \(p\), so we can create a bernoulli object, which is a super class of the rv_discrete type, that models a fair coin as shown.

p = 0.5 

fair_coin = bernoulli(p)

The fair_coin object can be used to simulate a number of coin flips, below we simulate 10 000 and plot the resulting histogram.

import numpy as np
import matplotlib.pyplot as plt

flips = fair_coin.rvs(10_000)

y, x = np.histogram(flips, bins=2, density=True)

fig, ax = plt.subplots()
ax.bar(x[::2], y, width=0.1)
ax.set_xlabel('$k$')
ax.set_ylabel('$P(X=k)$')
ax.set_xticks([0, 1])
ax.set_xticklabels(['Tails', 'Heads'])
plt.show()
../_images/8b219b08b7e7d350842702fe3f7ca98db06543d72134f3f83e08912785204c42.png

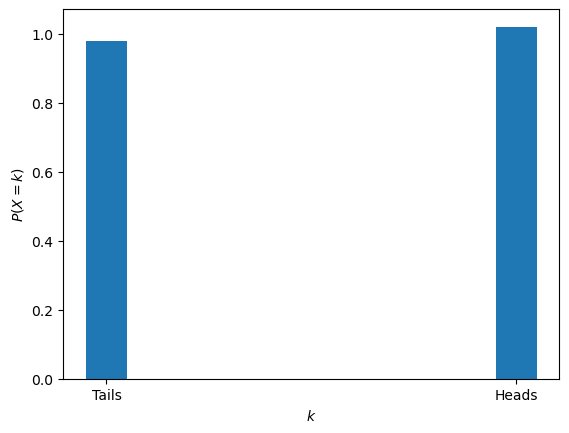
We can see, that over 10 000 observations, the coin appears fair. The rvs method samples random variables from the distribution. This method is available for any rv_discrete or rv_continous object.

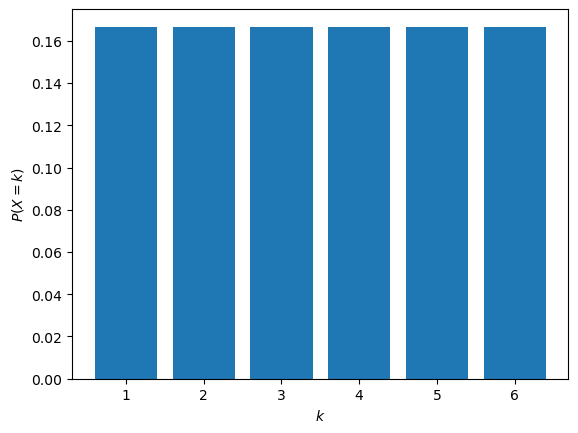
If we wanted to simulate rolling a fair dice, we could use a uniform discrete distribution. Each side of the fair dice is equally likely. The uniform discrete distribution in SciPy is called randint.

from scipy.stats import randint

low = 1
high = 7
fair_dice = randint(low, high)

We can plot the PMF of this distribution using the pmf method.

x = np.arange(low, high)

fig, ax = plt.subplots()
ax.bar(x, fair_dice.pmf(x))
ax.set_xlabel('$k$')
ax.set_ylabel('$P(X=k)$')
plt.show()
../_images/faabcd015212b8caf52546c140f48b169f26585f7c06080673b0196966844d9b.png

Continuous Distributions#

The rv_continuous object has many of the same features as the rv_discrete. So lets look first at the model for a normal distribution.

from scipy.stats import norm

mu = 0
sigma = 1
standard_normal = norm(mu, sigma)

x = np.linspace(-4, 4, 1000)

fig, ax = plt.subplots(1, 2, figsize=(8, 4))
ax[0].plot(x, standard_normal.pdf(x))
ax[0].set_xlabel('$x$')
ax[0].set_ylabel('$P(x)$')
ax[0].set_ylim(0, None)
ax[1].plot(x, standard_normal.cdf(x))
ax[1].set_xlabel('$x$')
ax[1].set_ylabel('$P(X \leq x)$')
ax[1].set_ylim(0, None)
plt.tight_layout()
plt.show()
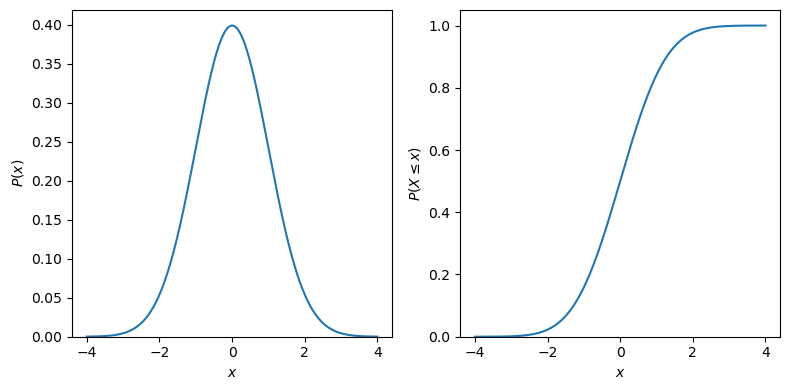
../_images/48430abae59a923eff10136a0fcca0289704ef04d4fd28dcfd8efcbe750d5cbd.png

Above, we plot the PDF and CDF for a standard normal distribution. This is a special type of normal distribution where the mean is 0 and the variance (and standard deviation) is 1.

These SciPy objects have a stats method, that can be used to find out the parameters of the distribution.

standard_normal.stats()

(0.0, 1.0)
Contents