Derivatives

Derivatives#

The derivative describes the rate of change of a curve and, at a given point on the curve, tells the gradient of the tangent line (see Fig. 18). Mathematically, where a one-dimensional curve is \(f(x)\), the derivative is defined as:

(29)#\[ f'(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x}. \]

That is to say that the derivative describes how \(f(x)\) changes at an infinitesimally small change in \(x\), \(\Delta x \to 0\).

How To Find a Derivative#

To investigate how to find a gradient, let’s consider a plot of \(f(x) = y = x^2\). We can plot this with Python.

import numpy as np 
import matplotlib.pyplot as plt

x = np.linspace(0, 1, 100)
y = x ** 2

fig, ax = plt.subplots()
ax.plot(x, y)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
plt.show()
../_images/4966a105d9d5bdd4e49d616c85898423848022a4451a0739c0c1db257d1c6d63.png

For this system, the gradient at any point on the plot, \(m\), can be calculated as the change in \(\Delta y / \Delta x\). We can describe the numerator of that function in terms of \(x\) alone,

\[ \Delta y = (x + \Delta x) ^ 2) - x^2. \]

Therefore, we can rewrite the gradient as,

\[ m = \frac{x^2 + 2x \Delta x + \Delta x^2 - x}{\Delta x}, \]

and then simply to get,

(30)#\[ m = 2x + \Delta x. \]

This means that as \(\Delta x \to 0\), the gradient tends to \(2x\). For example, for the plot above, at \(x = 0.5\), we can find the gradient.

gradient = 2 * 0.5
offset = 0.5 ** 2 - gradient * 0.5

fig, ax = plt.subplots()
ax.plot(x, y)
ax.plot(x, gradient * x + offset, '--', 
        label='First Derivative at 0.5')
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
ax.legend()
plt.show()
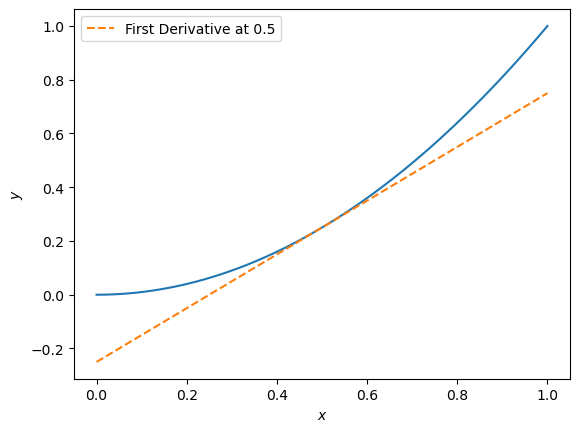
../_images/9fbffb98d8a32647ec56f9b8360262c660748afa50c10ad17befd7a1d5bb2a78.png

So, we can see the dashed line is at a tangent to the \(x^2\) line at \(x=0.5\).

Generalisation#

This result can be generalised with the following formula,

(31)#\[ \frac{\text{d}(x^n)}{\text{d}x} = nx^{n-1}, \]

which will give the gradient at any point along the curve.

Finding Derivatives in Python#

An interesting Python library that can be used for symbolic mathematics, which means maths with symbols, i.e., \(x\), \(y\), and \(z\) instead of specific numerical values, known as sympy. This library is designed explicitly for symbolic mathematics, which means that performing numerical calculations is generally speaking a bad idea. We present it here as a tool to aid understanding.

sympy can be used to find the derivative of a given function. For example, this can be used to compute the same derivative as computed above manually.

from sympy import symbols, diff

x = symbols('x')
diff(x ** 2, x)
\[\displaystyle 2 x\]

This library is a powerful tool that we will return to in this section.

Numerical Derivative Estimation#

We can also use Python to estimate the derivative explictly. For this, we compute the values of a function at \(x\pm \text{d}x\) and calculate the slope around \(x\), where \(\text{d}x\) is a very small value. For example, if we want to estimate the derivative of \(x^2\) at \(x=0.4\), we know from Eqn. (30) that the gradient will be \(0.8\).

dx = 1e-7
x = np.array([0.4 - dx, 0.4 + dx])
y = x ** 2
gradient = np.diff(y) / np.diff(x)
gradient

array([0.8])

The accuracy of this approach increases with decreasing values of dx. Let us see how differentiation can be used practically in our data science applications.

Contents